
最近惊喜发现刚买的笔记本电脑自带了一块RTX2050显卡,带2048个CUDA核心。那么研究一下并行计算,让这块显卡也发挥一下价值。
前缀和指一个数组的某下标之前的所有数组元素的和(包含其自身)。 前缀和分为一维前缀和,以及二维前缀和。 前缀和是一种重要的预处理,能够降低算法的时间复杂度;如求解子数组的最大/最小值、子数组和的平均值等问题,都可以用前缀和算法来高效地解决。
一维前缀和的公式:
1sum[i] = sum[i-1] + arr[i]
前缀和示例:

拿到前缀和之后的第一想法,就是拿CPU计算来手撕代码,这是非常简单的,见如下代码:
1void prefix_by_cpu(int32_t* input, ssize_t n, int32_t* output)
2{
3 int32_t sum = 0;
4
5 for (ssize_t i = 0; i < n; i++) {
6 sum += input[i];
7 output[i] = sum;
8 }
9}
1定义一个前缀和数组 output,长度与原数组相同。
2从前往后遍历原数组,依次计算前缀和,更新 output 数组。
3遍历完成后,output 数组中存储的即为原数组的前缀和。
使用CPU计算前缀和,一个循环就可以了,时间复杂度是O(n),其中n为数组的长度。
手里的RTX2050就要发挥威力了!通过检索学习互联网上前缀和计算的并行算法,我这里也想出来了一个不一样的计算方式如下:
1归约:按照"2的幂次方"进行分组进行数据的归约,如图中步骤"①=>③";
2计算:按照数据的坐标,进行数据的计算,如图中的"⑤";
使用并行计算的时间复杂度,可以缩减到O(log n),其中n为数组的长度。
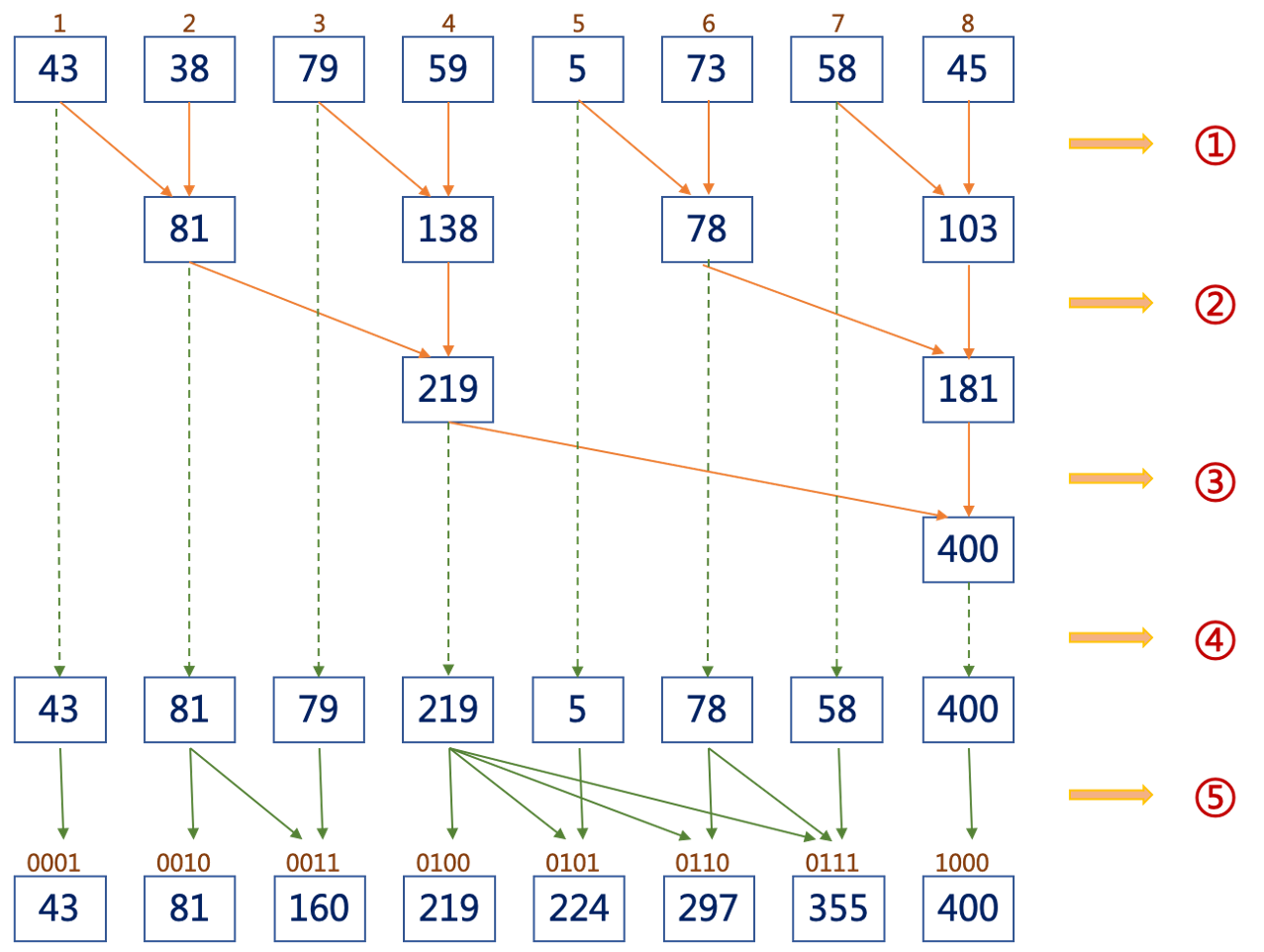
第一步按照2的幂次方进行数据归约,代码如下:
1int i = blockIdx.x * blockDim.x + threadIdx.x;
2
3for (ssize_t stride = 2; stride <= InputSize; stride *= 2) {
4 __syncthreads();
5 if (i > 0 && i % stride == (stride - 1) && i < InputSize) {
6 X[i] += X[i - stride / 2];
7 }
8}
此段代码是前缀和算法的核心部分:
1for (ssize_t stride = InputSize; stride >= 1; stride /= 2) {
2 __syncthreads();
3 if (i < InputSize && ((i + 1) % stride) == 0 &&
4 ((i + 1) % (stride * 2)) != 0 && power_of_2_d(i + 1) != i + 1) {
5 // 按照2的幂次方逐层进行计算
6 // 将偏移拆解为二进制字节码,如
7 // - 偏移为6的数据,二进制为0110,则计算和的偏移为:
8 // sum(6)=arr[4]+arr[4+2]
9 // - 偏移为7的数据,二进制为0111,则计算和的偏移为:
10 // sum(7)=arr[4]+arr[4+2]+arr[4+2+1]
11 int32_t sum = 0;
12 ssize_t pos = 0;
13 for (int x = InputSize; x > 0; x >>= 1) {
14 if ((x & (i + 1)) != 0) {
15 sum += X[x + pos - 1];
16 pos += x;
17 }
18 }
19 X[i] = sum;
20 }
21}
注 1:此段核心代码还是初稿,心中还有一些思路可以做更多的改进;
注 2:此段核心代码的计算方法,我搜遍全网目前还没有使用该思路的。 嗯嗯,专利走起~
将计算好的前缀和结果拷贝到输出的数组中,代码如下:
1__syncthreads();
2if (i < InputSize) { // copy 前InputSize字节
3 Y[i] = X[threadIdx.x];
4}
1void prefix_by_cuda(int32_t* input, ssize_t n, int32_t* output)
2{
3 int32_t *indev, *outdev;
4 uint32_t power = power_of_2(n);
5
6 printf("power=%u\n", power);
7
8 // 分别为input 和 output 申请设备内存,其中input数组保持2的幂次方对齐
9 cudaMalloc(&indev, sizeof(int32_t) * power);
10 cudaMalloc(&outdev, sizeof(int32_t) * n);
11
12 // 拷贝数据到设备内存的input数组,保持剩余可用空间被设置为零
13 cudaMemcpy(indev, input, sizeof(int32_t) * n, cudaMemcpyHostToDevice);
14 cudaMemset(indev + n, 0, power - n);
15
16 // 调用GPU计算前缀和
17 work_efficient_scan_kernel<<<64, 64>>>(indev, power, outdev);
18
19 // 将前缀和的结果拷贝到CPU内存
20 cudaMemcpy(output, outdev, sizeof(int32_t) * n, cudaMemcpyDeviceToHost);
21
22 // 释放设备内存
23 cudaFree(indev);
24 cudaFree(outdev);
25}
源代码路径: 点击这里
并行计算的思路与传统计算不太一样,脑子里要时刻想着GPU中那几千个核心的异步计算。通过对前缀和的研究,下一个研究的课题也在脑海中成型。这里预告一下: 应该是RLE编解码相关的主题。